Floating Point
移码表示
作用
传统的有符号数表示方法(如补码)需要特殊的符号位来表示正负数。而移码的优点在于它不需要显式的符号位,通过给值加上偏移量,使得负数和正数都可以通过无符号数的方式来表示。
移码表示有助于在进行数值比较、加法等运算时简化符号问题,因为它通过偏移量将整个范围都转换为非负数。
原理
移码的基本思想是通过给一个整数添加一个固定的偏移值(即移码)来消除负号,使得负数和正数都可以用非负数表示。具体来说:
- 移码值 = 实际值 + 偏移量 其中,偏移量(bias)通常是 2^(n-1),其中 n 是位数。
通常,在移码表示中,我们使用 2^(n-1) 作为偏移量,特别是用于表示整数或浮点数。
这个偏移量使得表示的范围从 0 到 2^n - 1,其中偏移量可以在值的负数部分加上一个固定的偏移,使得“零”值为偏移值。
IEEE 浮点标准
IEEE 标准 754建立于1985年,作为浮点运算的统一标准, 由所有主要CPU支持。
- 受数值问题驱动, 对于四舍五入、上溢、下溢来说是很好的标准
- 硬件很难快速制造, 在定义标准时,数值分析师比硬件设计师占主导地位
数字形式
在 IEEE 754 浮点数标准中,浮点数通常表示为:(–1)^s * M * 2^E
- 符号位 s 确定数字是负数还是正数
- 有效数字 M 通常是范围
[1.0,2.0)内的一个分数值 - 指数 E 按二次幂对值进行加权
编码
MSB 是符号位 s, exp 字段编码为 E (但不等于 E), frac 字段编码为 M (但不等于 M) 
表示方式
在浮点数表示法中(如 IEEE 754 浮点数标准),数值的表示方式分为 规格化数值、非规格化数值 和一些 特殊值。这些概念是理解浮点数表示、计算精度和溢出的关键。
在 IEEE 754 浮点数标准中, 偏移量(Bias)通常被表示为: Bias = (2^(k-1)) - 1, 其中 k 是指数位数。Bias(float) = 127, Bias(double) = 1023。
规格化数值
条件: exp ≠ 000…0 和 exp ≠ 111…1 时
指数值: E = Exp(exp 字段的无符号值) – Bias
用隐含的前导1进行编码: M = 1.xxxxx
.xxxxx: frac 字段的位数- 当 frac=00000 时最小 (M = 1.0)
- 当 frac=11111 时最大 (M = 2.0 – ε)

非规格化
条件: exp = 000…0时
指数值:E = 1 – Bias 用隐含的前导0进行编码: M = 0.xxxxx
.xxxxx: frac 字段的位数- 当 frac = 000…0, 表示不同的值 +0 和 –0
- 当 frac ≠ 000…0, 表示最接近 0.0 的数字, 等距
特殊值
条件: exp = 111…1时
当 frac = 000…0时, 可能表示正无穷(−1.0/−0.0), 负无穷(1.0/−0.0) 当 frac ≠ 000…0时, 表示不能确定数字值的情况, 非数字(NaN)

四舍五入
十进制
默认的舍入方式很难在不丢失精度的情况下获得任何其它类型的值, 一组正数的总和总是被高估或低估
当正好处于两个可能值的中间时, 四舍五入,使最低有效位数为偶数
- 7.8949999 7.89 (不到一半)
- 7.8950001 7.90 (高于一半)
- 7.8950000 7.90 (一半—向上舍入)
- 7.8850000 7.88 (一半—向下舍入)
二进制
最低有效位为0时为“偶数”, 当舍入位置右侧的位 = 100…2 为“一半”
| Value | Binary | Rounded | Action | Rounded | Value |
|---|---|---|---|---|---|
| 2 | 3/32 | 10.000112 | 10.002 | (<1/2—down) | 2 |
| 2 | 3/16 | 10.001102 | 10.012 | (>1/2—up) | 2 1/4 |
| 2 | 7/8 | 10.111002 | 11.002 | (1/2—up) | 3 |
| 2 | 5/8 | 10.101002 | 10.102 | (1/2—down) | 2 1/2 |
乘法
 符号位 s = s1 ^ s2, 有效数字 M = M1 * M2, 指数位 E = E1 + E2
符号位 s = s1 ^ s2, 有效数字 M = M1 * M2, 指数位 E = E1 + E2
如果 M ≥ 2,将 M 右移,增加 E。如果 E 超出范围,则溢出 。为了适合 frac 精度舍入M
加法
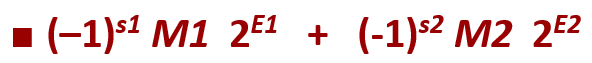
对于符号位 s 和有效数字 M, 取有符号数对齐和相加的结果。取较大的指数E
如果 M ≥ 2,将 M 右移,增加 E 。如果 M < 1,将 M 左移 k 位, 将 E 递减 k 位。如果 E 超出范围,则溢出。为了适合 frac 精度舍入M
转换
(double/float)2int: 截断小数部分。值将会向0截断。超出范围或 NaN 时未定义:通常设置为 TMin
int2double: 精确转换,只要 int 的字大小 ≤ 53 位
int2float: 将会遵守四舍五入
