Representation of Signed Numbers
最早的计算机ENIAC(埃尼阿克)采用十进制而不是二进制 二进制是由冯诺依曼体系结构规定的
计算机里的数据分两大类
- 数值数据:无符号整数、带符号整数、浮点数
- 非数值数据:位串(0和1组成)、字符(包括中文、英文等)
基础概念
真值
真正的值,即现实中带正负号的数
机器数
计算机内部用0和1编码的0/1序列 例如:unsigned char a = 254, 机器数则为2^8 - 2 = 11111100
数据表示
数值数据表示有三要素: 进位计数制, 定/浮点表示, 定点数的编码
进位计数制称进制。进制有很多种,计算机中,最重要的是十进制、二进制、十六进制、八进制,以及它们的相互转换
定点数的编码(原码、补码、反码)解决正负号问题, 其中反码已经不再使用在计算机的数字电路中只有加法器,没有所谓的减法器。计算机保存最原始的数字,是没有正负之分的,叫做无符号数字。
定/浮点主要解决小数点问题
原码
原码左边第一位存放符号,0表示正数,1表示负数。原码直观易懂、与真值转换容易, 但是也有很多缺点。
- 0的表示不唯一,不利于程序员编程
- 加减运算方式复杂不统一,电路设计更复杂
- 运算时需要额外对符号进行处理
例如:1 + (-1) = 0001 + 1001 = 1010 = -2 结果与正常的运算逻辑不符
反码
现代的计算机系统已经不使用反码了, 把"反码"当作历史概念和某些协议里的特定算法即可。
- 正数的反码保持原码不变:3 =
00000011(原码) =00000011(反码) - 负数除符号位外, 其余所有位数全部取反: -5 =
10000101(原码) =11111010(反码)
于是3 + (-5) = (-2)的计算过程为: 00000011 + 11111010 = 11111101
补码
计算机不同于人脑,计算机在碰到任何数字之前只根据最高位的符号位来判断正负性,0表示正数,1表示负数。
用8位二进制反码表示的话,其中有两个特殊的编码会出现: 00000000(+0)、11111111(-0)
其实,+0和-0代表的都是0。这样一来,0这个数字在计算机中的编码就不是唯一的了。对于计算机来说,这是绝对不行的,因为任何数字都只能有1个编码。
我们把0当成正数,这样0的编码就变成 00000000。那8位二进制表示的正数范围仍然是: +0 —— +127。
把负数整体向后挪动1位, 只要将8位二进制表示的负数范围变成:-128 —— -1,就能成功解决问题。
正数时,补码跟原码一样;负数时,补码就是原码符号位除外,其他位按位取反,再加1。
运算推导
假设运算器为4位,则模为2的4次方,等于16
- 0的补码为 0 + 16 = 0000 + 10000 = 0000 = 0
- 1的补码为 1 + 16 = 0001 + 10000 = 0001 = 1
- -1的补码为 -1 + 16 =
10000 – 0001=1111 – 0001 + 0001=1110 + 0001= 1111
计算真值
例如: 补码1001真值 = -2^3 + 2^0 = -8 + 1 = -7 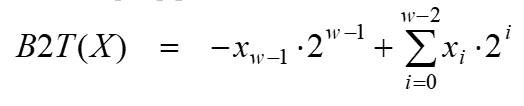
模运算系统
在一个模运算系统中,一个数与它除以“模”后的余数等价。
时钟是一种模12系统。假设钟表时针指向9点,要将它拨向7点,有两种拨法:
- 逆时针拨2格:
9 - 2= 7 - 顺时针拨10格:
(9 + 10) (mod 12)= 7
模12系统中,9 – 2 ≡ (9 + 10) (mod 12), –2 ≡ 10 (mod 12), 则称 -2的模12补码等于10
重要结论
- 运算器只有有限位,假设为n位,则运算结果只保留较低的n位,因此,其模为2^n
- 负数的补码 = 模减去它的绝对值
- 在确定模下,减 B 就等于加上 B 的补码,结果再取膜。
我们便可以用负数(十进制)的补码 来表示 负数的加法
